Ensembles apply to trajectories, not frames

It is common to initially think of ensembles as applying on a frame-by-frame basis. However, ensembles are only valid on trajectories, not individual frames. To explain this, let’s consider a couple simple common misconceptions.

Combining volume ensembles doesn’t combine volumes

It might seem like Ensemble(volume_A) & Ensemble(volume_B) should be the same as Ensemble(volume_A & volume_B). But this is absolutely not the case. We can see this easily by using PartOutXEnsemble as the example ensemble. PartOutXEnsemble(volume) creates an ensemble in which at least one frame must be outside of volume. So the difference between and-ing together the two ensembles vs. and-ing together the two volumes can be described like this:

• PartOutXEnsemble(volume_A) & PartOutXEnsemble(volume_B): there is at least one frame in the trajectory outside of volume_A, and at least one frame outside of volume_B. These two frames do not need to be the same frame.

• PartOutXEnsemble(volume_A & volume_B): there is at least one frame which is outside of volume_A & volume_B, which is the intersection of volume_A and volume_B.

Note that the second case does NOT mean that a single frame is simultaneously outside of both volume_A and volume_B: it is outside the intersection, not the union. If what you want is a ensemble of trajectories which contain at least one frame that is simultaneously outside of volume_A and outside of volume_B, you can write that as PartOutXEnsemble(volume_A | volume_B).

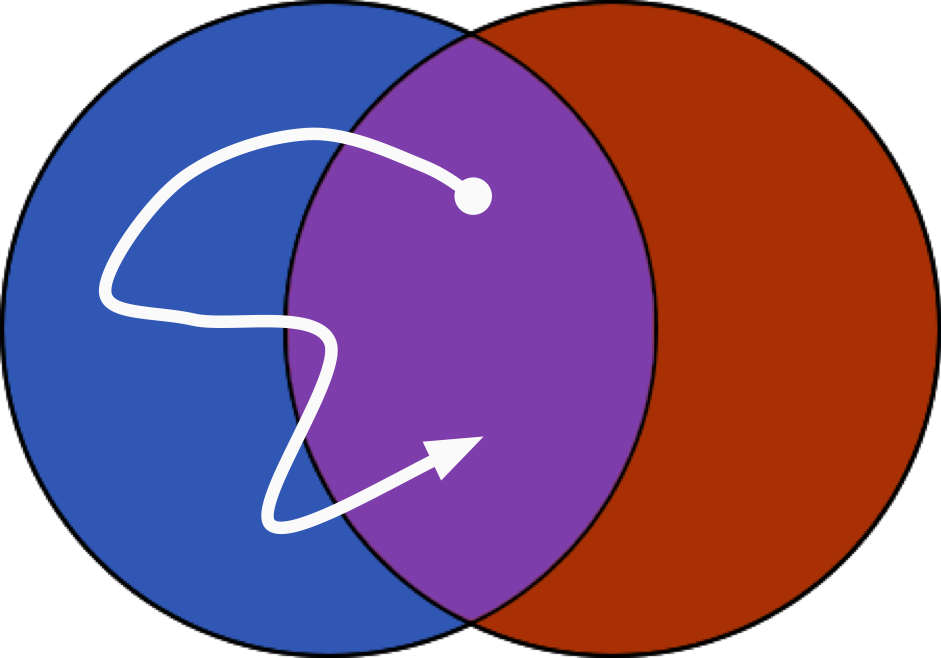
The above trajectory is in PartOutXEnsemble(volume_A & volume_B) but not in PartOutXEnsemble(volume_A) & PartOutXEnsemble(volume_B). To be in that ensemble, it would need to have a frame in the red area, or the outside both volumes in the white area. The volume given by volume_A & volume_B is the purple area, and some frames are outside of that.

Complementary frames do not generate the logical inverse ensemble

Another case where your intuition can lead you astray is when thinking about complementary and inverse ensembles. For example, since InXEnsemble(volume) consists of frames inside of volume and OutXEnsemble(volume) consists of frames outside of volume, you might mistakenly think that InXEnsemble(volume) | OutXEnsemble(volume) allows all trajectories.

However, if you think about the whole trajectory, you’ll see this is not the case. InXEnsemble requires that all frames be in the given volume; OutXEnsemble requires that all frames be outside the given volume. A trajectory tested with InXEnsemble(volume) | OutXEnsemble(volume) must satisfy one of the two ensembles: either all frames inside or all frames outside. It can not include a transition across edge of the volume.

OutXEnsemble is complementary to InXEnsemble in the sense that OutXEnsemble(volume) == InXEnsemble(~volume), but OutXEnsemble(volume) != ~InXEnsemble(volume). This again comes back to the statement in the previous section that combining volume ensembles does not combine volumes, because InXEnsemble(volume) | InXEnsemble(~volume) != InXEnsemble(volume | ~volume).

To find the actual logical inverse of an ensemble, we should return to its set-theoretic definition. For InXEnsemble, this is:

\[\forall t; x[t] \in V_x\]

where \(t\) is the time (frame number), \(x\) is the order parameter function which defines the volume, and \(V_x\) is the extent of the volume. To take the logical not of that, we apply the standard rules that \(\forall\) becomes \(\exists\) and \(\in\) becomes \(\notin\), giving us:

\[\exists t\ | \ x[t] \notin V_x\]

This is, of course, the definition for a PartOutXEnsemble. And if we think about this in words, it makes perfect sense: if the ensemble requires that all frames be in some volume, then the set of all trajectories which do not satisfy that ensemble would have at least one frame outside that volume.