TIS Analysis

OpenPathSampling tries to give reasonable default approaches to analyze results from transition interface sampling. These defaults are run through the TransitionNetwork objects, after using the rate_matrix method for that network. The main analysis sections of the main examples show how to use the default analysis.

However, sometimes you may want to customize the analysis, or you may want to develop new approaches to analyze the data. This document describes how the analysis tools in openpathsampling.analysis.tis work.

Note

Most of the presentation here is in terms of a simple \(A\to B\) reaction network. For the most part, the generalization to multiple states is straightforward. When it isn’t, we’ll provide more details.

To start, let’s look at way TIS calculates the rate. The fundamental equation is:

\[k_{AB} = \phi_{A_0} P_A(B|\lambda_0)\]

where \(\phi_{A_0}\) is the flux out of state \(A\) and through interface \(\lambda_0\), and the \(P_A(B|\lambda_0)\) is the conditional probability that a path ends in \(B\) (before any other state) given that it exits \(\lambda_0\). We refer to this conditional probability as the “transition probability” for the transition \(A\to B\). Note that the formally, \(\lambda\) should also be labeled by the interface set that it refers to (and in MSTIS, the state label is often used to stand in for the only interface set). In the \(A\to B\) transition, there is only one interface set, so there is no possibility of confusion.

This equation focuses on the rate, but one of the important advantages of TIS is that other quantities, such as projections of the committor probability or of the free energy landscape, can be obtained from the same information as the TIS rates by using the reweighted path ensemble.

All TIS simulations make this split. In the following, we’ll discuss the various ways to calculate the flux, and then we’ll discuss approaches for calculating the transition probability (which usually involves further splitting). But first, let’s introduce a glossary for the terminology and mathematical notation to be used.

Glossary

Term	Math Notation	Description
flux	\(\phi_{A_0}\)	frequency at which a path starting in \(A\) crosses the innermost interface \(\lambda_0\)
transition probability	\(P^\text{tot}_A(B | \lambda_0)\)	probability that a path that starts in \(A\) and crosses the innermost interface \(\lambda_0\) will next hit state \(B\)
(ensemble) crossing probability function	\(P_A(\lambda | \lambda_i)\)	probability that a path that starts in \(A\) and crosses (is sampled from) interface \(\lambda_i\) reaches \(\lambda\)
total crossing probability function	\(P^\text{tot}_A( \lambda | \lambda_0)\)	probability (calculated from all data) that a path that starts in state \(A\) and crosses the innermost interface \(\lambda_0\) will reach \(\lambda\)
conditional transition probability	\(P_A( B | \lambda_m)\)	probabiility that a path that starts in \(A\) and crosses (is sampled from) interface \(\lambda_m\) will next hit state \(B\)

The probabilities above can be separated along two axes. The first is whether the are a crossing probability (a function of some order parameter \(\lambda\)) or a transition probability (a number indicating the probability of ending in some state). The second axis is whether they are directly sampled during the simulation, or whether they are calculated from the full simulation data. This distinction is illustrated in the table below.

	Crossing probability function	Transition probability
Sampled	\(P_A(\lambda | \lambda_i)\)	\(P_A(B | \lambda_m)\)
Total	\(P^\text{tot}_A( \lambda | \lambda_0)\)	\(P^\text{tot}_A(B | A_0)\)

In the limit of infinite sampling, the sampled and calculated versions should be identical. That is, the crossing probability sampled from interface \(\lambda_0\), \(P_A(\lambda | A_0)\), would equal the total crossing probability \(P^\text{tot}_A(\lambda | A_0)\). And similarly, the conditional transition probability sampled from \(\lambda_0\), \(P_A(B | \lambda_0)\), would equal the total transition probability \(P^\text{tot}_A(B|\lambda_0)\).

Of course, the entire point of TIS is that infinite sampling is not possible. In fact, the very definition of the transition being a rare event is that, under feasible sampling, \(P_A(B | \lambda_0) \approx 0\). By sampling multiple path ensembles, TIS allows us to get a good estimate for \(P_A(B|\lambda_0)\) with much less sampling effort.

We typically only discuss the “total” examples (both total crossing probability and total transition probability) with the innermost interface as the condition. When it comes to the (sampled) conditional transition probability, we typically use the outermost interface (traditionally denoted with the subscript \(m\)).

For simple cases, the value of \(\lambda\) is the sole feature defining both states. In that case, the transition probabilites are equivalent to crossing probabilities evaluated at \(\lambda = \lambda_B\). However, in most realistic systems \(\lambda\) only serves as an estimate of reaction progress, and the actual state definitions include additional requirements.

---

Calculating the flux

We provide two main approaches for calculating the flux. The first approach is to directly calculate the flux, using either the DirectSimulation or TrajectoryTransitionAnalysis tools in OPS. This is relatively simple, and since you are likely to have run MD to ensure that your state is stable (and to select a location for the innermost interface), it is likely that you’ll already have enough data to get very precise results. When doing this, you’ll use the DictFlux object to store the flux.

The second approach is to calculate the flux using the minus interface. This isn’t possible if there is more than one interface set per initial state (as with MISTIS). This approach also tends to give larger errors; usually, you try to minimize how often you do the minus move, which reduces the statistics in this approach. However, this is the default (when possible), and can be explicitly selected by using the MinusMoveFlux object.

• An example of how to use the DirectSimulation object to determine the flux is given in the MISTIS example. The flux result returned by DirectSimulation can be used as input to a DictFlux.

• An example of how to use the TrajectoryTransitionAnalysis object to calculate the flux can be seen in one of the OPS additional examples. The flux returned from that can easily be turned into the correct format for the DictFlux object in order to use it for TIS analysis.

• Using the MinusMoveFlux is the default when it is possible. Details on how to use this are in the example notebook for the TIS analysis.

Calculating the transition probability

The other part of the TIS equation is the transition probability. This is where we actually get into TIS-specific analysis. In TIS, as with many “splitting” methods, the overall transition probability is broken into smaller transitions between different waypoints (“interfaces” in TIS terminology):

\[P^\text{tot}_A(B|\lambda_0) = \prod_{i=0}^{m-1} P_A(\lambda_{i+1}|\lambda_{i})\ P_A(B|\lambda_m)\]

There are a few ways that this can be calculated. What we term the “standard” approach involves calculating the crossing probability \(P_A(\lambda | \lambda_i)\) for each interface \(\lambda_i\), and using a combining procedure (WHAM by default) to create the total crossing probability \(P^\text{tot}_A(\lambda | \lambda_0)\), set \(\lambda = \lambda_m\) in that, and then use \(\prod_{i=0}^{m-1} P_A(\lambda_{i+1}|\lambda_i) = P^\text{tot}_A(\lambda_{m} | \lambda_0)\). The superscript “tot” is to distinguish the total crossing probability, which is computed based on all ensembles, from the crossing probability sampled from ensemble \(\lambda_0\) (see below). Finally, we calculate \(P_A(B|\lambda_m)\) (the “conditional crossing probability” to \(B\), given interface \(\lambda_m\)), and multiply these to get to transition probability.

Other approaches include the path-type analysis, and per-ensemble histograms (i.e., a coarser estimate of \(P(\lambda|\lambda_0)\), only obtaining estimates when \(\lambda\) is at an interface boundary.) These have not yet been implemented in OPS, but will be soon.

Total crossing probability

As discussed above, the quantity \(\prod_{i=0}^{m-1} P_A(\lambda_{i+1}|\lambda_i)\) is calculated from the total crossing probability \(P^\text{tot}_A(\lambda | \lambda_0)\). In particular, it is determined from the individual ensemble crossing probabilities \(P_A(\lambda | \lambda_i)\), which are sampled during the simulation.

Conditional transition probability

The conditional transition probability is \(P(B|\lambda_m)\), the probability of reaching state \(B\) given that the path was sampled from the outermost interface, \(\lambda_m\). Note that, in the case of multiple states, the only difference between calculating the rate for \(A\to B\) and \(A\to C\) is that the conditional transition probability changes.

The example notebook on the TIS analysis framework includes examples of how to create the TotalCrossingProbability, ConditionalTransitionProbability, and TransitionProbability objects.

Putting it all together: TISAnalysis objects

As discussed previously, the full TIS analysis always involves splitting the rate into flux and transition probability. The TISAnalysis objects maintain this split, and also cache the results from other parts of the analysis. This caching is useful both to speed up the overall analysis and to provide access to intermediate results for further investigation.

The plain TISAnalysis object just requires a flux calculation and a transition probability calculation. However, when performing analysis according to the “standard” approach, it is better to use the StandardTISAnalysis class. This caches several results, and is therefore much more efficient than manually setting up the same approach using a plain TISAnalysis object.

There are many options for setting up the StandardTISAnalysis; see the documentation of that class for more details. A few simple examples are shown in the following example notebook:

The example notebook about the TIS analysis subsystem includes an example of the StandardTISAnalysis, as well as a description of how to set up the more genreal TISAnalysis object.

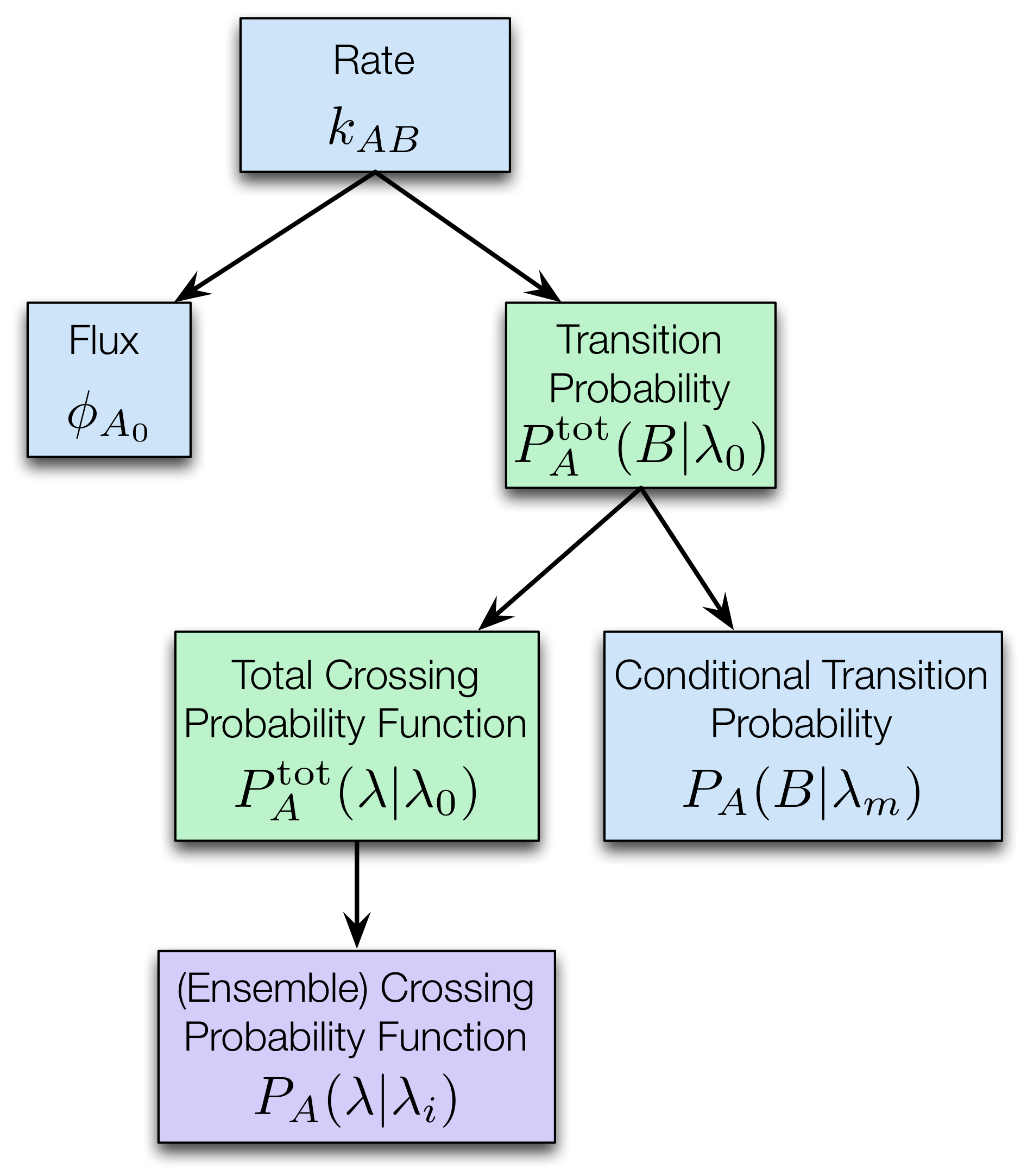
Summary: Visual overview of the standard analysis

In the image below, we provide a visual overview of the standard analysis. Each box represents a specific part of the calculation, and the name, as well as mathematical symbol, are included in the box. The color of the box indicates how many of these objects there are in the OPS standard analysis: blue boxes indicate one per reaction network, green boxes indicate one per transition, and purple boxes indicate one per ensemble.